Структуры данных в программировании: что это и какие бывают

Выполняя повседневные задачи, программисты работают с различными структурами данных, для каждой программы она своя. О самых популярных вариантах структуры, их особенностях и способах применения подробно расскажем в этой статье.

Что такое структура данных и для чего она нужна

Структура данных — это форма организации и хранения информации в компьютерной программе. Она повышает эффективность управления с помощью модификации и обработки.

Благодаря структурам данных можно:

• Логически структурировать и группировать информацию, делая код более понятным и легко поддерживаемым.

• Хранить уникальные элементы, избегая дублирования информации (например, через хеш-таблицы).

• Оптимизировать процесс поиска, добавления, удаления и обновления данных.

• Экономно использовать память, например, через битовые и компактные массивы.

• Упростить выявление и устранение ошибок.

Классы структур данных

На практике выделяются основные структуры данных:

1. Примитивная. Обладает фиксированной памятью и представляет простые значения: целые числа, символы и прочее.

2. Сложная. Позволяет хранить множество значений и работает с более сложными операциями: добавление, удаление, поиск, сортировка данных и т. д. Сюда относятся массивы, списки, векторы и другие типы структур.

Среди сложных выделяются:

1. Линейная. Характеризуется сохранением элементов, которые идут один за другим и доступны в определённой последовательности. Примерами линейных структур данных являются массивы, списки, стеки и очереди.

2. Нелинейная. Элементы могут иметь несколько связей, образуя иерархические, сетевые или произвольные структуры. Примерами нелинейных структур являются деревья и графы.

В линейных можно выделить такие подтипы:

1. Статистическая. Имеет фиксированный размер памяти, что ускоряет доступ к выбранным элементам.

2. Полустатистическая. Комбинация статических и динамических элементов, обеспечивающая баланс между эффективностью использования памяти и гибкостью работы с данными.

3. Динамическая. Здесь размер и структура могут меняться динамически. Это делает управление данными более гибким и позволяет проводить операции с конкретными элементами в любой момент.

Основные алгоритмические типы структур данных

Хеш-таблицы

Неупорядоченная коллекция пар «ключ — значение», где каждый ключ уникален. Хеш-таблица используется для реализации структур данных (map, dict, set и т. д.), особенно полезна для хранения, поиска и добавления элементов.

Операции с хеш-таблицами:

• Вставка. Позволяет добавить в хеш-таблицу элемент с определённым ключом. Сначала ключ преобразуется в хеш-значение, затем размещается в соответствующей ячейке таблицы.

• Удаление. Удаляет элемент с заданным ключом из хеш-таблицы. Сначала ключ преобразуется в хеш-значение, после чего проводится сама операция.

• Поиск. Помогает найти элемент в хеш-таблице через уникальный ключ.

В хеш-таблицах можно проводить следующие действия:

• Обновление. Меняет значение существующего в таблице элемента без переиндексации его ключа.

• Подсчёт элементов. Показывает, сколько элементов находится в хеш-таблице.

• Разрешение коллизий. Применяется, когда несколько ключей преобразуются в одно и то же хеш-значение. Ошибки корректируются через операции «Поиск» и «Вставка».

Где применяются хеш-таблицы:

• Реализация словарей и ассоциативных массивов.

• Кеширование данных или вычислений.

• Маркировка посещённых URL.

• Быстрый поиск и индексации данных (контакты, номера телефонов и т. д.) в CPaaS-сервисах вроде Exolve.

• Управление кешем объектов в приложениях и играх.

• Основа во многих базах данных для хранения большего объёма данных.

Массивы

Это структура, которая позволяет последовательно хранить несколько элементов одного и того же типа. Перейти к этим элементам можно через индекс — числовое значение определённой позиции, которое начинается с 0. При этом массивы бывают одномерными и двухмерными, ими может быть каждый элемент.

Задача массива — организовать удобную сортировку данных или поиск соответствующего набора значений.

Операции с массивами:

• Добавление. Предназначена для вставки нового элемента в конец существующей структуры данных.

• Обновление. Позволяет менять и присваивать новые значения элементам.

• Удаление. Можно сжимать, удаляя элементы.

• Сортировка порядке возрастания или убывания элементов, например, через алгоритмы быстрой или пузырьковой сортировки.

• Копирование элементов.

• Объединение. Для создания новых массивов с элементами из двух или больше исходников.

Где применяются массивы:

• Решение матричных задач.

• Применение алгоритма сортировки.

• Реализация стеков, очередей, хеш-таблиц.

• Планирование работы процессора.

• Создание справочной таблицы в компьютерах.

• Обработка речи, где каждый речевой сигнал представляет собой массив.

• Работа с системами управления баз данных: учёт книг, журналов или статей, учеников и студентов, голосов и решений и т. д.

• Создание компьютерных игр вроде онлайн-шахмат, с сохранением прошлых и текущих ходов игрока для указания позиции фигур.

Связный список

Непримитивная структура, создающая коллекции элементов в последовательном порядке. В этом формате узлы хранятся в несмежных ячейках памяти. Списки бывают односвязными, со ссылкой на следующий объект, и двусвязными — в том числе со ссылкой на предыдущий объект.

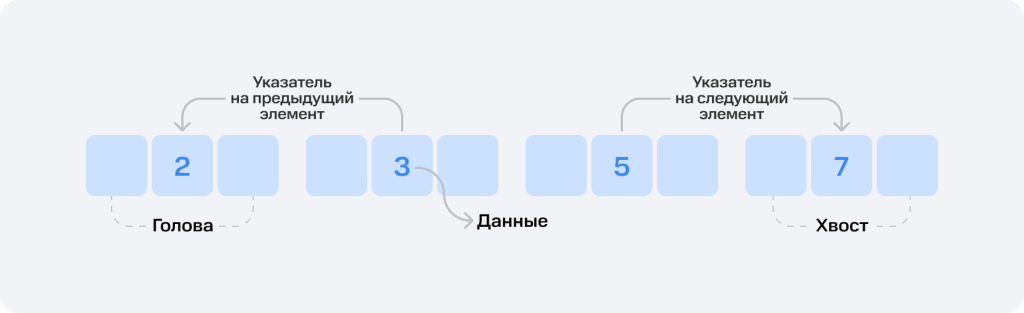
Это гибкая структура, где можно взаимодействовать с элементами списка без предварительного выделения фиксированного объёма памяти, как это делается в тех же массивах.

Операции со связанными списками:

• Инициализация. Инициировать список можно через создание головного узла. Каждый новый узел содержит значение и ссылку на следующий фрагмент.

• Вставка. Данные можно добавлять в начало, конец или обозначенную позицию связанного списка.

• Удаление. Делается через обновления ссылки предыдущего узла, чтобы та указывала на следующую ячейку списка.

• Поиск. Поиск нужного элемента начинается с головного узла и распространяется на следующие ячейки до тех пор, пока подходящий элемент не будет найден.

• Обновление. Проводится путём изменения данных, которые находятся в выбранном элементе.

• Обход. По узлам связанного списка можно перемещаться, начиная с головного узла и следуя ссылкам на следующие элементы, вплоть до конца всего списка.

• Обращение списка. Связанный список можно обратить вспять, обновив ссылки каждого узла таким образом, чтобы они указывали на предыдущий, а не на следующий элемент.

Где применяются связные списки:

• Выполнение арифметических операций с длинными целыми числами.

• Представление разреженных матриц.

• Связанное размещение файлов.

• Отображение контейнеров изображений (для просмотра прошлых, текущих и следующих картинок).

• Циклическое планирование для отслеживания ходов в многопользовательских играх.

• Упорядоченная связь песен в плейлисте и т. д.

Стек

Это линейная структура, которая функционирует по принципу LIFO, где последний добавленный элемент будет удаляться или извлекаться первым. К примеру, при открытии нескольких окон в Windows, активным останется именно последнее задействованное окно.

Операции со стеком:

• Добавление. Элемент добавляется на вершину и заменяет прежнее значение.

• Удаление. Выталкивание всех элементов из стека, что приводит к его очистке и восстановлению пустого состояния.

• Чтение головного элемента. Извлечение значения, которое было добавлено последним и находится в верхней части стека.

Также со стеком можно проводить следующие действия:

• Просмотр. С помощью этой операции верхний элемент можно осмотреть, не удаляя его.

• Размер. Позволяет просмотреть количество элементов.

• Поиск. Находит, возвращает на позицию или сообщает об отсутствии конкретного элемента.

• Проверка на пустоту или заполненность. Определяет наличие или отсутствие данных в стеке.

Где применяются стеки:

• Вычисление и преобразование арифметических выражений.

• Управление памятью.

• Обработка вызовов функций.

• Преобразование выражений из инфиксных в постфиксные.

• Воспроизведение следующей или предыдущей песни.

• Отслеживание ранее посещённых сайтов в браузере.

• Формирование журнала вызовов в мобильном приложении.

Очередь

Структура линейного порядка, в отличие от стека, основана на принципе FIFO, где вначале обрабатывается первый сохранённый элемент данных.

Очередь отлично справляется с управлением заданий для ОС, учётом товаров на складе, обработкой сетевых пакетов и т. д.

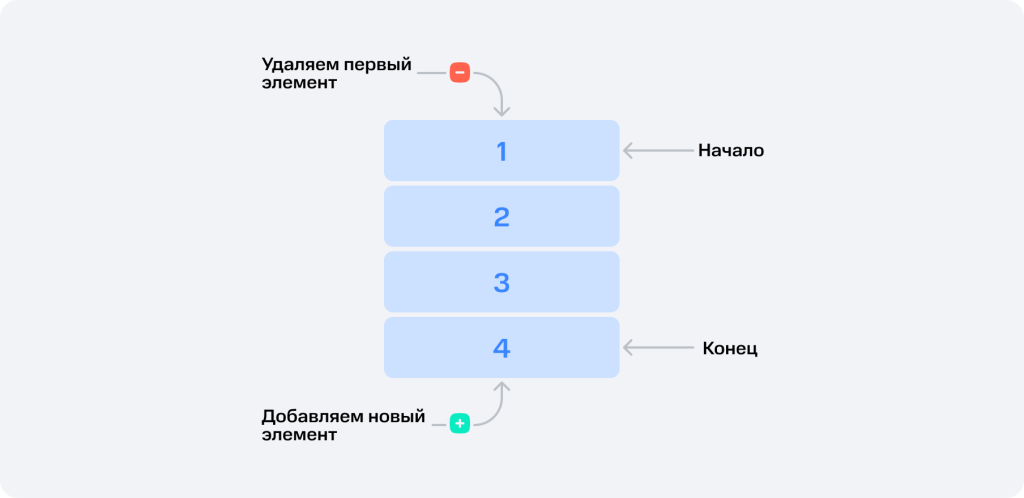
Операции с очередью:

• Добавление. Элемент можно добавлять в конец до момента обработки.

• Удаление. Позволяет извлечь и обработать элемент из начала очереди.

• Front. Чтение или получение значения, находящегося в начале, без его удаления.

• Rear. Чтение или получение значения элемента, находящегося в конце очереди, без его удаления.

Где применяется очередь:

• Обработка трафика веб-сайта.

• Планирование и учёт запросов к общему ресурсу: распечатка на принтере, планирование задач процессора и т. д.

• Обработка прерывания, планирование заданий, переключение приложений в ОС.

• Асинхронная передача данных.

• Загрузка нескольких фото или видео и т. д.

Дерево

Иерархическая структура данных с разветвлённой системой элементов. Самый верхний узел дерева называется «корневым» — он ведёт к «родительским» узлам, которые делятся на «дочерние». Структура завершается «листами» — конечной точкой без «дочерних» узлов. Все элементы дерева соединены «рёбрами».

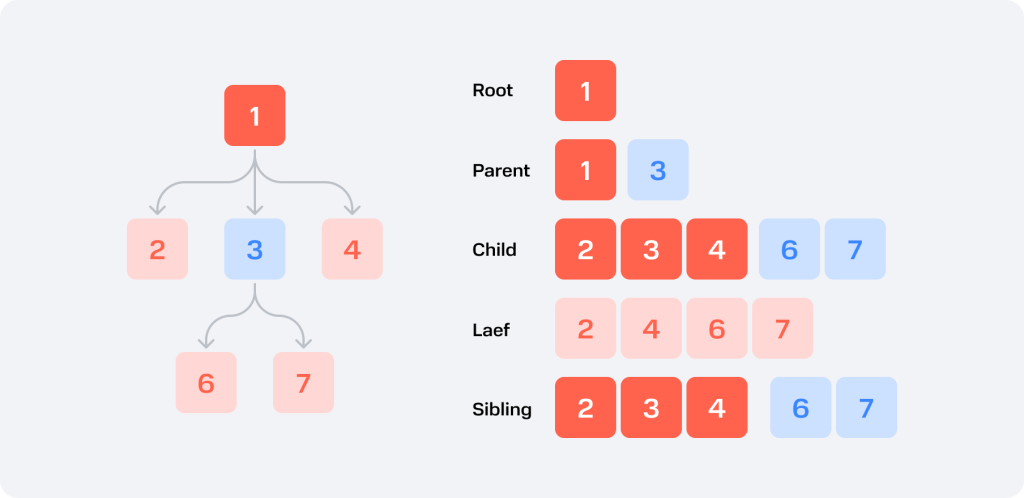
Деревья бывают бинарными, красно-чёрными, AVL и т. д. Каждый из видов обладает уникальными свойствами и способом применения. У любого дерева:

• В каждый узел, кроме корневого узла, входит одна ветвь.

• Существует узел, в который не входит ни одна ветвь.

Операции с деревьями:

• Вставка. Позволяет добавить новый узел в соответствии с правилами, присущими конкретному типу дерева. В двоичном поисковом дереве новый узел вставляется с условием сохранения порядка элементов.

• Балансировка. В некоторых типах деревьев (AVL, красно-чёрные) можно проверить, насколько сбалансированы и равномерны «рёбра».

• Обход. Помогает посетить все узлы дерева в определённом порядке. Для этого можно использовать прямой, обратный, симметричный метод обхода.

• Поиск. Находит узел по заданному ключу или значению. Процедура начинается с корня и рекурсивно движется вниз до получения результата.

• Удаление. Удаление узла из дерева и корректировка структуры для поддержания баланса или других свойств.

Где применяются деревья:

• Моделирование и управление поведением персонажей в видеоиграх.

• Добавление индексов в базы данных.

• Структурирование файловой системы.

• Создание и организация иерархии задач и заданий в системах управления проектами.

• Представление синтаксической структуры программного кода в компиляторах и анализаторах.

• Создание иерархических меню и древовидных структур навигации.

Граф

Нелинейная абстрактная структура данных, которая состоит из фиксированного конечного набора узлов или вершин. Соединена рёбрами — линиями, сцепляющими узлы всей структуры.

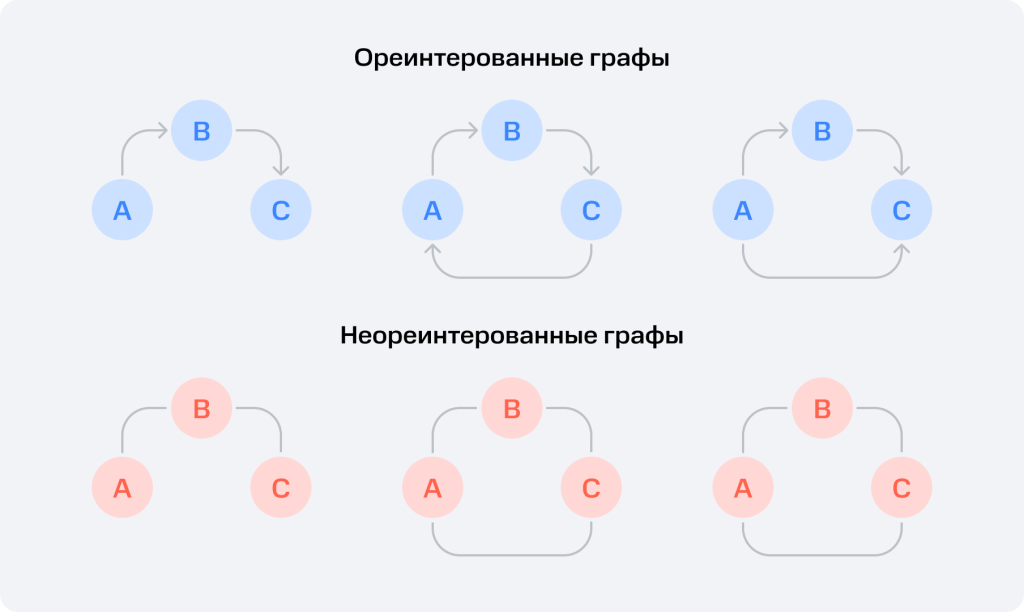
Графы широко применяются в алгоритмах и структурах данных, например в компьютерной графике, маршрутизации в сетях и прочих областях программирования.

Операции с графами:

• Добавление вершины. Создаёт в графе новую вершину. Операция нужна для формирования нового элемента или сущности в модели.

• Добавление ребра. Связывает две вершины, задаёт направление и при необходимости вес ребра. Операция помогает моделировать отношение между вершинами.

• Удаление вершины. Исключает из графа выбранную вершину и связанные с ней рёбра.

• Удаление ребра. Разрывает соединение между двумя вершинами, отменяя указанное ребро. Полезно, когда связь между вершинами более неактуальна.

• Проверка свойств графа. Включает в себя анализ различных характеристик графа: направленность, ацикличность, связность, наличие циклов и других свойств — для обеспечения корректности и соответствия требованиям задачи.

• Вычисление кратчайших путей между вершинами. Это делается с помощью алгоритмов Дейкстры, Флойда — Уоршелла и прочих методов.

Где применяются графы:

• Представление потока вычислений.

• Распределение ресурсов в операционной системе.

• Моделирование дружеских связей и взаимодействий между пользователями социальных сетей.

• Оптимизация дорожных сетей, планирования маршрутов, управления транспортным движением и GPS-навигации.

• Представление биохимических сетей, геномных данных и анализа взаимодействия белков в молекулярной биологии.

• Отражение синтаксических и семантических отношений между словами в тексте.

• Бронирование номеров в гостиницах.

Заключение

Существует множество классов и типов структур данных — каждый со своими особенностями, преимуществами и недостатками. При выборе оптимальной модели управления информаций в первую очередь нужно руководствоваться индивидуальными особенностями конкретного проекта вроде объёма данных, уровня потенциальной нагрузки и масштабируемости.